Range Addition II

Problem

Given an m * n matrix M initialized with all 0's and several update operations.

Operations are represented by a 2D array, and each operation is represented by an array with two positive integers a and b, which means M[i][j] should be added by one for all 0 <= i < a and 0 <= j < b.

You need to count and return the number of maximum integers in the matrix after performing all the operations.

Example 1:
Input: 
m = 3, n = 3
operations = [[2,2],[3,3]]
Output: 4
Explanation: 
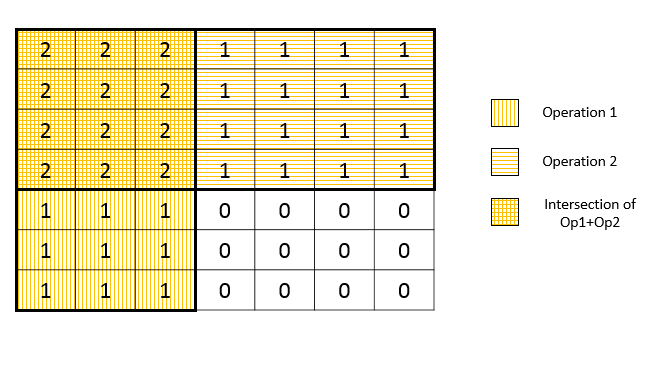
Initially, M = 
[[0, 0, 0],
 [0, 0, 0],
 [0, 0, 0]]

After performing [2,2], M = 
[[1, 1, 0],
 [1, 1, 0],
 [0, 0, 0]]

After performing [3,3], M = 
[[2, 2, 1],
 [2, 2, 1],
 [1, 1, 1]]

So the maximum integer in M is 2, and there are four of it in M. So return 4.

Note:

• The range of m and n is [1,40000].
• The range of a is [1,m], and the range of b is [1,n].
• The range of operations size won't exceed 10,000.

Solution

Brute force solution, completely following the instructions of problem (Time Limit Exceeded in Leetcode)

public class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        int[][] matrix = new int[m][n];
        for (int[] op: ops) {
            for (int i = 0; i < op[0]; i++) {
                for (int j = 0; j < op[1]; j++) {
                    matrix[i][j]++;
                }
            }
        }
        int res = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == matrix[0][0]) res++;
            }
        }
        return res;
    }
}

Smart solution thinking about the "cover of range"

public class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        for (int[] op : ops) {
            m = Math.min(m, op[0]);
            n = Math.min(n, op[1]);
        }
        return m * n;
    }
}

Analysis

The problem's description looks complicated but the solution is very easy to understand
In the first solution, we simply follow the instruction of problem in every step
Since we know the first element will be operated every time, we know it is the max value
So we loop the entire matrix and increment the res if we find value equals to matrix[0][0]

The second solution uses the idea of "thinking about the entire problem first"
If we finish all the operation from ops we know that every time a rectangle area of elements are increased
Therefore, to find the count of max value, we need to find out the most cover area of that rectangle
This is to find the min range of the operation from ops
At the end, we get the area of this range and return it as our result
The picture below explains this process much more clearly

Complexity:

• First solution: O(x n m) time and O(m n)* space, where x is the length of operations
• Second solution: O(x) time and O(1) space (no extra space is used)